Generating hexagonal meshes on spheres
Introduction
This post will briefly go over the steps necessary for tesselating a sphere with hexagons (and 12 pentagons).
There are many advantages to using hexagons instead of squares/triangles when tesselating a sphere. Hexagons have great visual appeal, there is fewer artifacts than with squares, and their adjacency neighbourhoods are better than those of triangles. But compared to squares/triangles, tiling a sphere with hexagons requires the most work. The 2 sections below will show how to subdivide an icosahedron to get a triangular mesh, and then how to tesselate that into hexagons (and 12 pentagons).
Icosahedron subdivision
We start with a convex regular icosahedron, more commonly known as a 20 sided dice. The icosahedron consist of 12 vertices, and 20 triangles/faces. Any polyhedron made up of triangles could be used for this technique, but most would create large artifacts.

At this stage we need to divide each triangle. The 20 initial triangles, will then create 80 new triangles. This division step is repeated until the desired resolution is achieved. For reference; 8 divisions will yield a triangular mesh with 1310720 triangles, and 655362 vertices.
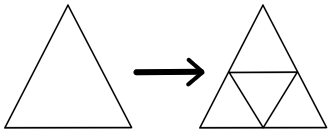
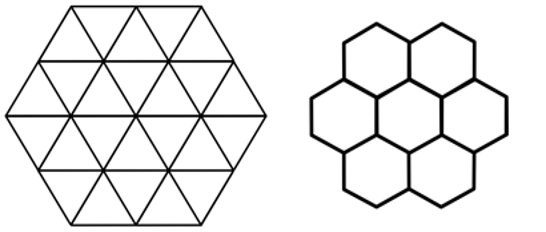
After 3 divisions the triangular mesh looks like this.

Polygon tesselation
We now have a triangular mesh of sufficient resolution. The next step is to tesselate it into polygons.
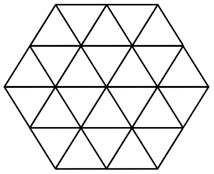
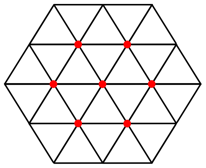
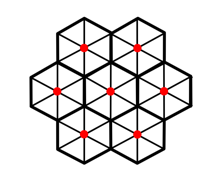
The vertices in the triangular mesh, will become the center vertices for each polygon in the new tesselated mesh. In the image below, each red dot will be the center of a hexagon.
In order to create the boundry between the polygons we need more vertices. The blue dots will be the vertices making up the border of each polygon. The blue dots are simply formed by calculating the average vertex for each triangle.
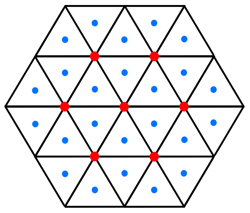
We not connect the blue dots to create the borders, this is shown as a green line.
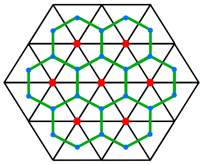
We have now created the hexagons. But we need to fill the hexagons with triangles, in order to be able to create geometry for use in graphics. We do this by simply connecting the border vertices (blue dots) with the center vertex (red dot).
We are now done creating the hexagonal mesh for use on spheres. The same steps apply for the 12 pentagons that are created. If the implementation is made properly, now extra care needs to be taken for the pentagons. In other words, the same functionality is used for generating pentagons and hexagons. This image shows the mesh cleaned up, compared to what we started with.
And here is a final example of a hexagonal mesh, made with 3 subdivisions.

Get Orbis Multiplex
Orbis Multiplex
A complex simulation oriented strategy and management game on planetary scale
| Status | On hold |
| Author | Robin Johansson |
| Genre | Simulation, Educational, Strategy |
| Tags | 4X, Automation, Economy, Generator, Management, Procedural Generation, Singleplayer |
| Languages | English |
More posts
- Hexagonal grid | 0.2.0.0Aug 07, 2022
- Automatic tick progression | 0.1.6Mar 25, 2022
- Transportation network | 0.1.5Mar 09, 2022
- Ground water diffusion from rivers | 0.1.4Feb 18, 2022
- Updated landscape evolution algorithm | 0.1.3Feb 03, 2022
- Minor industry additions | 0.1.2Jan 28, 2022
- Industry production added to gameplay | 0.1.0Jan 26, 2022
- Version 0.0.11Dec 19, 2021
- Version 0.0.10Sep 24, 2021

Leave a comment
Log in with itch.io to leave a comment.